|
|
|
|
薛定谔 |
薛定谔( E.Schrodinger ,1887- 1961) 奥地利物著名的理论物理学家,量子力学的重要奠基人之一。 薛定谔在德布罗意提出的物质波的基础上,把物质波表示成数学形式,建立了称为薛定谔方程的量子力学波动方程。 |
薛定谔方程 |
|
| 由于微观粒子有波粒二象性 → 运动状态呈现概率波的特征; 如何找到描述概率波的状态的波函数 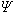 ? ?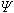 一般是空间和时间的函数,即 一般是空间和时间的函数,即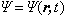 微观粒子在不同条件下( 例如,处于不同的外场中 ) 的运动状态是不同的,这就要用各种具体的波函数来描述其运动。因此波函数  所满足的方程中应反映出微观粒子所处的不同条件。
所满足的方程中应反映出微观粒子所处的不同条件。1926 年,薛定谔找到了波函数 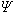 满足的方程,从而建立了研究微观粒子运动规律的学科——量子力学。
满足的方程,从而建立了研究微观粒子运动规律的学科——量子力学。若微观粒子的质量为 m, 微观粒子在外力场中的势能函数为 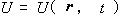 , ,则薛定谔方程为 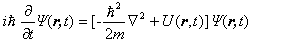
式中
|
|
定态薛定谔方程 |
|
| 常常遇到微观粒子的势能函数 U
与时间 t
无关的稳定的势场问题,例如 自由运动的粒子 U = 0 氢原子中的电子 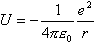 势场稳定时,波函数 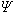 可以分离为一个空间坐标的函数和一个时间函数的乘积,解薛定谔方程也变得更为简单了。 可以分离为一个空间坐标的函数和一个时间函数的乘积,解薛定谔方程也变得更为简单了。例如: 对于一维运动的情况,波函数可写成 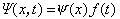 将其代入一维薛定谔方程 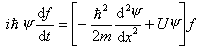 两边除以 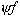 ,得 ,得 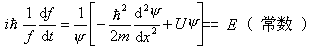 于是,可得两个方程: 1、变量为 t 的方程 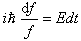 其解为 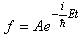 (A
是待定复常数)—— (1) (A
是待定复常数)—— (1)2、变量为 x 的方程 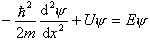 即 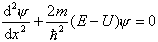 ——
(2) ——
(2)E —— 具有能量的量纲,以后可知 E 是粒子的能量,它包含粒子的动能和势能,但不包含静能。 由上面可以看出 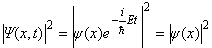 即此时概率密度可以用 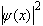 来表示,它与时间无关。
来表示,它与时间无关。
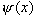 称为定态波函数,(2)式是 称为定态波函数,(2)式是
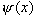 满足的方程,称为定态薛定谔方程。 满足的方程,称为定态薛定谔方程。对势能函数 U 与时间 t 无关的一维定态问题,只须解定态薛定谔方程(2)式,再与(1)式相乘即可得波函数 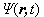 。
。 |
|
意义 |
|
|
薛定谔方程在量子力学中占有极其重要的地位,它与经典力学中的牛顿运动定律的价值相似。 薛定谔方程是量子力学中描述微观粒子运动状态的基本定律,在粒子运动速率远小于光速的条件下适用。 经典力学中,已知力 F 及 x0、v0,可由牛顿方程求质点任意时刻状态。 量子力学中,已知起始状态、能量 E和薛定谔方程,可求粒子波函数、粒子在某一体积中概率、定态时系统能量。 要使上式解得的波函数是合理的,对y 要求的条件:
|
|
|
量子数 |
|
|
要解出薛定谔方程的ψ和E,必须要满足一定的条件,才能使解是合理的,因此,在求解过程中必需引进n , l , m 三个量子数。 这三个参数的取值和组合一定时,就确定了一个波函数。
|
|

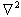 为拉普拉斯算符
为拉普拉斯算符