|
|
|||||
|
|
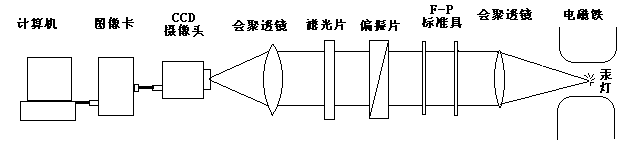
1896年,荷兰科学家塞曼发现当光源放在足够强的磁场中时,原来的一条光谱线分裂成几条光谱线,分裂的谱线成分是偏振的,分裂的条数随能级的类别而不同,后称塞曼效应
。 塞曼效应更进一步涉及了光的辐射机理,因此人们把它看成是继 X 射线之后物理学最重要的发现之一。 |
||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|||||
|
|
|||||
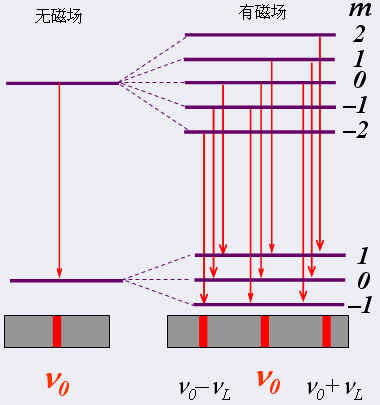
| 谱线分裂,表明能量差的变化。要了解谱线在磁场中的分裂现象,就要考察磁场对光源的作用。 | |||||
|
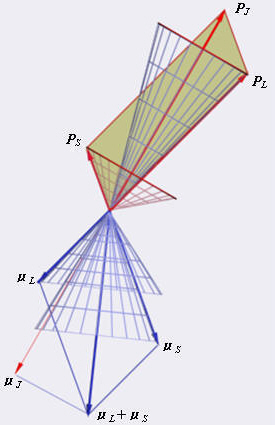
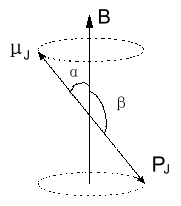
1、原子的总磁矩与总动量矩的关系 |
|||||
|
前面我们知道,原子中的电子不但有轨道运动,而且还有自旋运动。因此,原子中的电子具有轨道角动量PL和轨道
磁矩
μL
,以及自旋角动量 Ps 和自旋磁矩
μS
,它们的关系为: 式中 L ,S分别表示轨道量子数和自旋量子数, e,m 分别为电子的电荷和质量。
原子核有磁矩,但它比一个电子的磁矩要小三个数量级,故在计算单电子原子的磁矩时可以把原予核的磁矩忽略,只计算电子的磁矩。 |
|||||
|
|||||
|
|
|||||
设谱线是由 E1和 E2两能级间跃迁产生的,此谱线的频率由下式确定: |
|||||
|
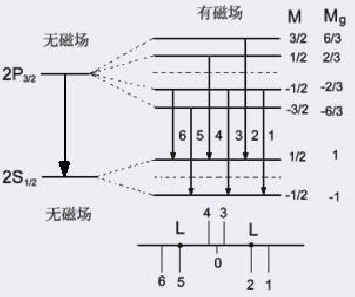
3、塞曼效应的选择定则 |
|||||
|
跃迁必须满足以下选择定则:
(2)
当ΔM=±l,产生 σ 线,为光振动方向垂直于磁场的线偏振光, |
|||||
|
塞曼效应证实了原子具有磁距和空间取向量子化的现象,至今塞曼效应仍是研究能级结构的重要方法之一。
|
|||||