|
|
|
|
|
1914年,夫兰克(J.Franck)和赫兹(G.Hertz)用电子与稀薄气体原子碰撞的方法,测量原子的激发电势和电离电势,证实原子有不连续的能级存在。二人因此于1925年获诺贝尔物理学奖。 |
|
|
|
|
|
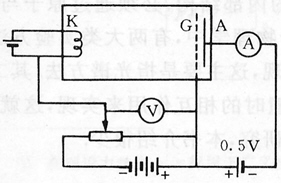
充有低压水银蒸汽的玻璃管,电子与汞原子碰撞,使汞原子吸收电子能量而激发。 K:热阴极,发射电子 KG区:加速电子,使之与 Hg 原子碰撞 GA区:使电子减速,能量大于一定数值的电子穿过 G 达到 A 形成电流。 |
|
|
|
|
根据玻尔理论,原子只能较长久地停留在一些稳定状态(即定态),其中每一状态对应于一定的能量,各定态的能量是分立的。当激发态的原子在回到基态时,它将以光子的形式放出它所减少的这部分能量。光子的频率
为 ν =(E2-E1)/h ,其中E2表示发光之前原子的能量,E1表示发光之后的能量。 原子只能吸收或辐射相当于两定态间能量差的能量。如果处于基态的原子要发生状态改变,所具备的能量不能少于原子从基态跃迁到第一激发态时所需要的能量。 |
|
|
夫兰克—赫兹实验是通过具有一定能量的电子与原子碰撞,进行能量交换而实现原子从基态到高能态的跃迁。 设 Hg 原子的基态能量为E1,第一激发态的能量为E2,则 Hg 原子的基态与第一激发态的能量差为ΔE=E2-E1; 初速度为零的电子在加速电压U0的作用下,获得能量为eU0,获得能量的电子与 Hg 原子发生碰撞: 当电子能量eU0<E2-E1时,电子与 Hg 原子只能发生弹性碰撞,由于电子质量比 Hg 原子质量小得多,电子能量损失很少。 如果eU0≥E2-E1时,则电子与 Hg 原子会产生非弹性碰撞。 Hg 原子从电子中取得能量ΔE=E2-E1,由基态跃迁到第一激发态,eU0=ΔE。相应的电位差U0即为 Hg 原子的第一激发电位。 |
|
|
在充有 Hg 原子气体的夫兰克—赫兹管中,电子从阴极射线管中发射出,在加速电压UGK的作用下,电子在阴极K和栅极G之间加速。 在板极A 和栅极G 之间有减速电压UAG,管内电位分布如下图所示。当电子通过KG空间进入GA 空间时,如果能量大于eUAG就能达到板极形成板流。电子在KG空间与 Hg 原子发生了非弹性碰撞后,电子本身剩余的能量小于eUAG,则电子不能到达板极,板极电流将会随栅极电压增加而减少。 |
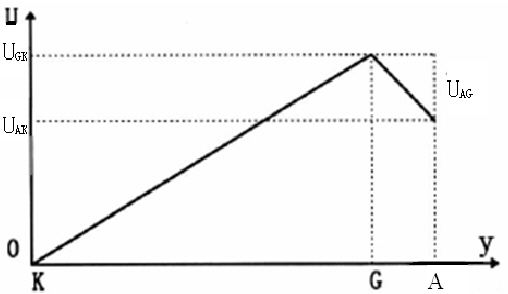 夫兰克—赫兹管管内电位分布 |
|
|
|
| 实验时使UGK逐渐增加,仔细观察板极电流的变化,将观察到的结果画出图线,如下图所示。 | |
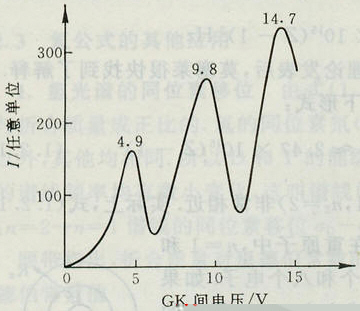 |
随着UGK的增加,电子能量增加,当电子与 Hg 原子碰撞后还留下足够的能量,可以克服GA空间的减速场而到达板极A 时,板极电流又开始上升。如果电子在KG空间得到的能量eU=2ΔE 时电子在KG空间会因二次非弹性碰撞而失去能量,而造成第二次板极电流下降。在UGK较高的情况下,电子在跑向栅极的路程中,将与 Hg 原子发生多次非弹性碰撞。 只要UGK=nU0(n=1,2,…), Hg 原子就会多次与电子发生非弹性碰撞而发生跃迁,在IA-UGA曲线上电流将出现多次下降。通过测量曲线上相邻两峰(或谷),对应的UGK之差,即可求出 Hg 原子的第一激发电位。 如果 Hg 原子从第一激发态又跃迁到基态,这就应当有相同的能量以光辐射的形式放出,其波长可以通过公式hν=eU0计算出来,实验中确实能观察到这些波长的谱线。 |
|
|
|
|
原子存在能级
|
|
: