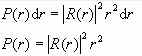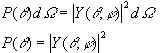| 几率也称为“概率”和“或然率”,是概率论中最基本的概念。 |


 |
| 在社会和自然界中,某一类事件在相同的条件下可能发生也可能不发生,这类事件称为“随机事件”。如掷骰子,设骰子落地后每一面朝上的可能性均相同。即1、2、3、4、5、6朝上的可能性是一样的,而出现六个数字中的每一个数字都是随机事件。再如一只口袋装两个黑球,一个白球和一个红球,这四个球的大小、形状、重量完全一样,从口袋中任取一球,所取得的是红球也是一个随机事件。不同的随机事件发生的可能性的大小是不相同的,几率就是用来表示随机事件发生的可能性大小的一个量。很自然地把必然发生的事件的几率规定为1,并把根本不可能发生的事件的几率规定为零,而一般随机事件的几率是介于零与1之间的分数,例如,在上面的第一个例子中,出现,1,2,3,4,5,6的几率均是1/6,而第二例中,取出黑球的机率为1/2,而取出白球和红球的几率均为1/4 。几率越大便表示该事件发生的可能性越大。 |
几率密度和电子云 |
|
电子在核外空间出现机会统计的结果得到电子的几率密度分布形象的称为电子云。 在距原子核很远的地方,电子出现的几率几乎等于零,意味着不可能在那里发现电子。有些非常靠近核的区域其几率也是零,也是无法发现电子的区域。 |
电子云的角度分布 、径向分布 |
|
氢原子中处于定态(n、l、ml)的电子分布的概率密度
在玻尔半径 r =a1 处,基态 n
=1 的电子概率密度最大, |
|
从角度波函数的形式可知,
但概率按
|
|
将 电子云图并不表示电子像一团云雾罩在原子核周围,而是电子概率分布的一种形象化描述。 下面 是径向分布概率密度的电子云图。
|