|
玻尔原子模型
|
|

玻尔 |
玻尔在卢瑟福原子有核模型的基础上,结合原子光谱的经验规律,根据牛顿力学的理论,把普朗克的量子论(量子化的概念)和爱因斯坦于1905年提出的光子假说应用到原子系统,建立了“定态原子模型”(轨道模型)。 |
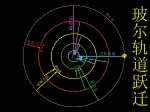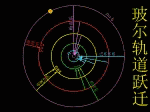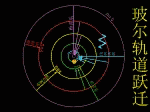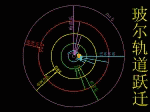 |
|
玻尔于1913年提出了三个基本假设
|
定 |
(1)定态假设: |
这一条是经验性的,但它是波尔对原子结构理论的重大贡献,因为他对经典概念作了巨大的修改,从而解决了原子稳定性的问题。
|
|
原子中的电子只能在一些特定的圆轨道上运动而不辐射电磁波,电子处于某种“定态”,并具有一定的能量
(E1、E2、E3…)。 |
|
量 |
(2)量子化条件:
|
这一条所表述的角动量量子化,是人为设定的,后来知道,它可以从德布罗意假设自然得出。 |
电子以速度v在半径为r的圆周上绕核运动时,只有满足 2πrmv = nh ,n =1,2,3,……(n为主量子数)的轨道才是稳定的。
或Pφ=
rmv = nh/2π
= n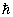 ,即:电子只能在一系列不连续的轨道上运动,这些轨道角动量Pφ等于 ,即:电子只能在一系列不连续的轨道上运动,这些轨道角动量Pφ等于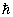 的整数倍
。 的整数倍
。 |
|
法 |
(3)频率法则: |
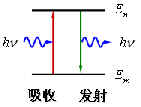 |
这一条是从普朗克量子假设引伸来的,因此是合理的,它能解释线光谱的起源 |
| 原子在两个能量状态间跃迁时,需辐射或吸收一定频率的光子,光子的能量由这两种定态的能量差
hν=En-Em
决定。(h为普朗克常量
) |
|
|
玻尔氢原子模型
|
|
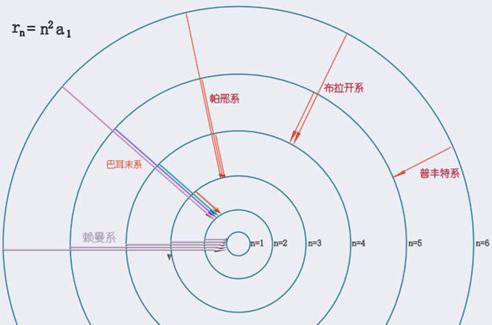
玻尔将这三个假设和卢瑟福原子模型结合在一起,推导出氢原子的大小和能级并解释了光谱。
rn
= n2a1,
a1=0.529埃 ,n=1,2,3,……
En = E1/
n2,
E1=-13.6电子伏, n=1,2,3,……
|
|
|
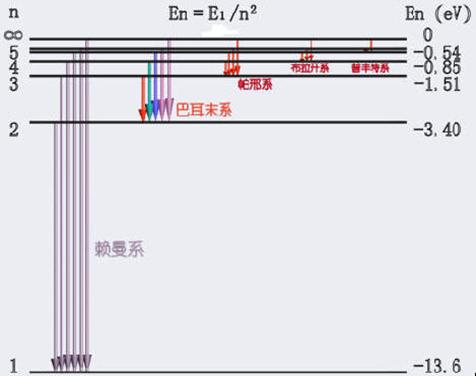 |
能级图中水平线表示实际存在的能级,右边用电子伏特标度。
n=l是最低能量状态即基态,原子最稳定。
n>1时,
是激发态能级。
由于能级和主量子数平方 n2 反比,随
n 增大,能级排布越来越密,当 n→∞时,成为连续区域,这是因为电离了的电子可具有任意的动能。
基态氢原子的电离能为13.6eV。
光谱线的发射是由于原子从一个高能级E2跃迁到低能级E1的结果,因此,各能级之间的垂直距离表示跃迁时以电磁辐射形式所释放的能量。 |
|
| n |
谱线记号 |
测量值 |
计算值 |
| 3 |
Ha |
6562.10 |
6562.08 |
| 4 |
Hb |
4860.74 |
4860.80 |
| 5 |
Hg |
4340.10 |
4340.00 |
| 6 |
Hd |
4101.20 |
4101.30 |
氢原子光谱的理论与实验的精确符合,证明了玻尔理论的正确性。 |
|
|
玻尔模型局限
|
|
(1)逻辑缺陷:以经典理论为基础,加上与经典理论不相容的量子化假设(半经典、半量子)。
(2)无法解释:多电子原子的光谱、谱线的强度、光谱线在磁场中的分裂等。
|




