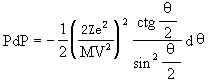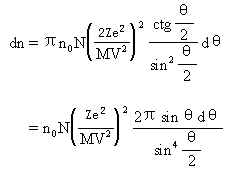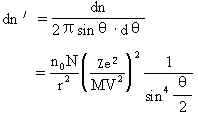α 粒子的散射
　
    下图描述了 α 粒子通过金箔的散射情况
　

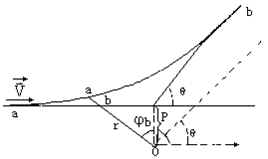
    假设距原子核很远的地方，α 粒子沿直线 αb 以速度 V 运动，以 P 表示直线 ab 与原子中心O（即原子的正电荷 Z 所在的地方）的最短距离。P被称为“瞄准”距离，可由理论力学应用电学知识计算证明，在 α 粒子与电荷  Z 之间存在着库仑相互作用力的情况下，α 粒子沿双曲线运动。而α粒子轨道的偏转角θ（双曲线的渐近线之间的角）为下式决定：

                                    

式中 M 是 α 粒子的质量，金原子核的质量和 α 粒子的质量相比较，可以看作是无穷大。由上式可知，“瞄准”距离P愈小，偏转角θ愈大。对于不同的“瞄准”距离，α 粒子的轨道形状可有如图a、b、c所示的三种情况。

           

        P 小到一定程度时，θ＞π/2，即 α 粒子与原子碰撞后可能被弹回。这种情况往往称为 α 粒子背向散射。

    假定一束平行的 α 粒子穿过金箔，并设单位时间内通过单位横截面的粒子数为n0。我们可以计算单位时间内有多少个粒子的偏转角是在给定的θ与θ+dθ之间。

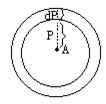
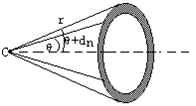
    设偏转角θ与“瞄准”距离P对应，而偏转角θ+dθ与“瞄准”距离P—dP对应。在此情况下，偏转角在θ～θ+dθ之间的粒子，是那些穿过以Α为中心，以P为半径所作的宽为dP的环的面积中的粒子如图所示。这样的粒子数目等于n。dS，式中dS为环的面积。如果金箔每单位面积有N个原子，则单位时间内其偏转角在θ与θ+dθ之间的α粒子的总数为 dn=n0NdS
    此关系式是在每一个α粒子只偏转一次的条件下才正确，而这个条件在金属箔足够薄时是能够实现的。环的面积dS近似地等于2πPdP。所以有 dn=2πn0NPdP

由

 

得
　

将上式微分，得出

显然

　

     

    式中Z是原子核的电荷数（原子序数）。dn表示单位时间内散射角在已知值θ与θ+dθ之间的粒子数目。换句话说dn是单位时间内在开放角为2θ和2（θ+dθ）的二锥体之间的空间内飞行的α粒子数目。
    如果我们以这两个锥体的顶点c为球心，作一半径为r的球，则这两个锥体在球面上截出的面积为2πrsinθ·rdθ=2πr2sinθ· dθ的区域，如左图所示的阴影部分。所有dn个粒子都射在这区域的面积上。因而落在单位面积上的粒子数目

       
                

　

　

　
原子核的大小
    根据卢瑟夫的核式结构模型，可以估计出原子核的线度不超过10-15米，它的这一线度也是由散射实验确定的。