|
|
|||||||||||
|
电子沿轨道运动时,具有轨道动量矩和轨道磁矩,产生磁场,电子还具有与其自旋角动量相联系的固有磁矩,产生另一磁场。由于这两种磁场的相互作用,产生附加的能量,这能量同Pl与Ps的相对取向有关。 取向应当服从空间量子化条件,由于电子自旋有两种方式,Ps相对于Pl的可能取向只有两种,与此两种可能取向相对应的有两种不同的附加能量 。因此,每一个光谱项分裂为两个。
由此可见,原子体系的能量不仅取决于n、l、s,还取决
|
|||||||||||
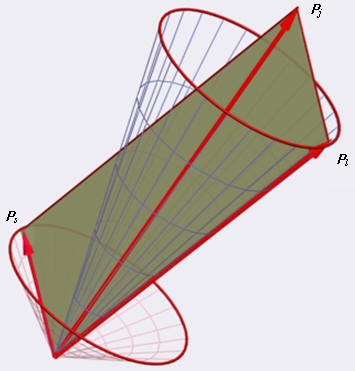 |
当用矢量模型来研究电子轨道矩和自旋矩合成时,电子的总角动量
根据量子力学的结果,在矢量加和过程中,
|
||||||||||
|
原子能级通常用光谱项符号 n2S+1LJ 来表示。 |
n
是指光学电子的主量子数; L 是该原子的总角(动量)量子数,L=0、1、2、3、4、5、……通常分别用大写符号S、P、D、F、G、……代表; 2S +1是表示谱线多重性的符号,S是核外光学电子的总自旋量子数。 |
||||||||||
|
例如 2S十1称为光谱项的多重性,因为每一个光谱项可有2S十1个不同的 J 值,通常把 J 值注在光谱项的右下角,例如3P 2、3P 1、、3P 0依次表示J=2、1、0,这样的符号称为光谱支项。每一个光谱项包含有 2S+1 个光谱支项。由于L和S的电磁相互作用,各光谱支项的能级微有不同,在光谱中形成 2S+1 条距离很近的线,这样的线叫做多重线。例如 2S+1=2 称为双重线,2S+1=3 称为三重线,等等。 以上讨论只适用于L≥S的场合,当L<S时,每一个光谱项只有2L+1个光谱支项,但是 2S+1 仍叫做多重性,所以多重性并不—定代表光谱支项的数目。 |
|||||||||||
| 我们可用原子矢量模型来讨论多电子原子的运动状态。多电子原子的运动状态可用下列量子数来表征: | |||||||||||
|
|||||||||||